![]() 反比率函数与几何
反比率函数与几何
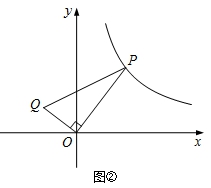
1.如图![]() ,反比率函数
,反比率函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,射线
,射线![]() 与反比率函数图象交于另一点
与反比率函数图象交于另一点![]() ,射线
,射线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 轴,垂足为
轴,垂足为![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值及直线
的值及直线![]() 的分析式;
的分析式;
(![]() 3)如图2,
3)如图2,![]() 是线段
是线段![]() 上方反比率
上方反比率![]() 函数图象上一动点,过
函数图象上一动点,过![]() 作直线
作直线![]() 轴,与
轴,与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
![]()
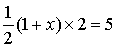

分析:(1)
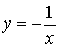
∵反比率函数![]() (
(![]() )的图象经过点
)的图象经过点![]()
∴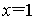 ,∴
,∴![]() [来源:学§科§网]
[来源:学§科§网]
(2)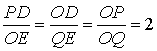
∵点![]() 在反比率函数
在反比率函数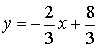 的图象上[来源:学科网ZXXK]
的图象上[来源:学科网ZXXK]
∴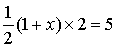 ,∴点
,∴点![]()
过![]() 作
作![]() 于
于![]() ,则
,则![]()
∴![]()
∵![]()
![]() ,∴
,∴![]()
∴
∴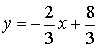 ,∴
,∴![]() ,∴
,∴![]()
设直线![]() 的分析式为
的分析式为![]()
∴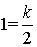 解得
解得
∴直线![]() 的分析式为
的分析式为
(3)设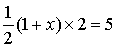 (
(![]() ),则
),则
则
∴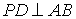
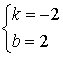
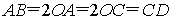
当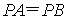 时,
时,![]() 的面积有最大值,最大值为
的面积有最大值,最大值为![]()
2.如图,点![]() ,
,![]() 在反比率函数图象上,
在反比率函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求反比率函数的表达式;
(2)连接![]() ,在
,在![]() 轴上是不是存在一点
轴上是不是存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,若存在,求出
,若存在,求出![]() 点坐标;若没有,请说明理由.
点坐标;若没有,请说明理由.
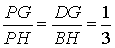
分析:(1)由题意,得 解得
解得
∴![]() ,
,![]()
设反比率函数的表达式为![]()
将![]() 代入
代入![]() ,得
,得![]()
∴反比率的表达式为![]()
(2)

∵![]() ,
,![]() ,
,![]() 轴,
轴,![]() 轴
轴
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∵![]() ,∴在线段
,∴在线段![]() 上和线段
上和线段![]() 的延
的延![]() 长线上必存在满足条件的
长线上必存在满足条件的![]() 点;在线段
点;在线段![]() 的延长线上没有满足条件的
的延长线上没有满足条件的![]() 点
点
设![]()
①当点![]() 在线段
在线段![]() 上时
上时
![]() ,
,![]()
![]()
![]()
![]() ,∴
,∴![]()
∴![]()
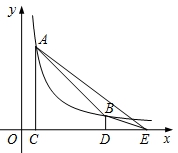
②当点![]() 在线段
在线段![]() 的延长线上时
的延长线上时
![]() ,
,![]()
![]()
![]()
![]() ,∴
,∴![]()
∴![]()
综上所述,![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]()
3.如图,已知反比率函数![]()
![]() ,
,![]() 是常数)的图象经过点
是常数)的图象经过点![]() 和点
和点![]() ,点
,点![]() 的横坐标大于点
的横坐标大于点![]() 的横坐标,
的横坐标,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)若点![]() 的纵坐标为
的纵坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,求反比率函数的分析式;
,求反比率函数的分析式;
(2)求证:![]() .
.
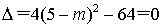
分析:(1)∵点![]() 的纵坐标为
的纵坐标为![]() ,
,![]()
∴点![]() 的纵坐标为
的纵坐标为![]()
∵点![]() 的横坐标为
的横坐标为![]() ,∴
,∴![]()
∵反比率函数![]() 的图象经过点
的图象经过点![]()
∴![]() ,∴
,∴![]()
∴反比率函数的分析式为![]()
(2)设![]() ,
,![]() ,其中
,其中![]()
∴![]() ,
,![]() ,
,![]() ,
,![]()
∴ ,
,![]()
∴![]()
又∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
4.如图,直线![]() 与双曲线
与双曲线![]() (
(![]() ,
,![]() )交于点
)交于点![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位长度后,与
个单位长度后,与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() (
(![]() ,
,![]() )交于点
)交于点![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)连接![]() ,求四边形
,求四边形![]() 的面积.
的面积.
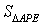
分析:(1)
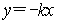
作![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,
,![]() 轴于
轴于![]()
则![]()
∵![]() ,∴四边形
,∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
∵![]() ,∴
,∴![]()
∴![]() ,
,![]()
∵点![]() 在直线
在直线![]() 上,∴设
上,∴设![]()
则![]() ,
,![]() ,∴
,∴![]()
∵![]() 、
、![]() 两点在双曲线
两点在双曲线![]() (
(![]() ,
,![]() )上
)上
∴![]()
解得![]() (舍去)或
(舍去)或![]()
∴![]() ,
,![]()
∴![]()
(2)![]()
![]()
![]()
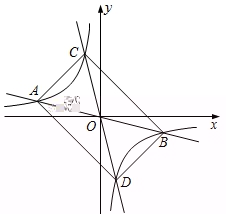
5.如图,点![]() 在双曲线
在双曲线![]() (
(![]() )上,直线
)上,直线![]() 交双曲线
交双曲线![]() (
(![]() )于点
)于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交双曲线
交双曲线![]() (
(![]() )于点
)于点![]() ,直线
,直线![]() 交双曲线
交双曲线![]() (
(![]() )于点
)于点![]() ,直线
,直线![]() 交双曲线
交双曲线![]() (
(![]() )于点
)于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)![]() 与
与![]() 是不是相等,请说明理由
是不是相等,请说明理由
(3)若![]() ,求点
,求点![]() 的坐标.
的坐标.

分析:(1)

设直线![]() 的分析式为
的分析式为![]()
可得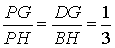 ,
,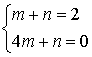
∴![]() 是
是![]() 的中点
的中点
同理可证![]() 是
是![]() 的中点
的中点
∴![]() 是
是![]() 的中位线
的中位线
∴![]()
(2)
当点![]() 在点
在点![]() 下方时,点
下方时,点![]() 在点
在点![]() 下方,连接
下方,连接![]()
∵![]() ,∴
,∴![]()
∵![]() 是
是![]() 的中点,∴
的中点,∴![]()
∴![]()
当点![]() 在点
在点![]() 上方时,点
上方时,点![]() 在点
在点![]() 上方,连接BE
上方,连接BE
∵![]() ,∴
,∴![]()
∵![]() 是
是![]() 的中点,∴
的中点,∴![]()
∴![]()
(3)①当点A在点E下方时,点B在点D下方
∵![]() ,
,![]()
∴![]()
∴点![]() 的纵坐标是点
的纵坐标是点![]() 纵坐标的
纵坐标的![]() 倍
倍
∴点![]() 的纵坐标是点
的纵坐标是点![]() 纵坐标的
纵坐标的![]() 倍
倍
作![]() 于
于![]() ,
,![]() 于
于![]()
则![]() ,∴
,∴![]()
![]()
∴![]()
设![]() ,则
,则![]()
∵![]() ,∴
,∴![]() ,
,![]()
∴ ,解得
,解得![]()
∴![]() ,∴
,∴![]()
②当点![]() 在点
在点![]() 上方时,点
上方时,点![]() 在点
在点![]() 上方
上方
∵![]() ,
,![]()
∴![]()
∴点![]() 的纵坐标是点
的纵坐标是点![]() 纵坐标的
纵坐标的![]() 倍
倍
∴点![]() 的纵坐标是点
的纵坐标是点![]() 纵坐标的
纵坐标的![]() 倍
倍
作![]() 于
于![]() ,
,![]() 于
于![]()
则![]() ,∴
,∴![]()
∴![]()
设![]() ,则
,则![]()
∵![]() ,∴
,∴![]() ,
,![]()
∴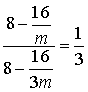 ,解得
,解得![]()
∴![]() ,∴
,∴![]()
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]()
6.如图①,直角三角形![]() 中,
中,![]() ,
,![]() 平行于x轴,
平行于x轴,![]() ,
,![]() ,反比率函数
,反比率函数![]() (
(![]() )的图象经过点A.
)的图象经过点A.
(1)直接写出反比率函数的分析式;[来源:Zxxk.Com]
(2)如图②,![]() 在(1)中的反比率函数图象上,其中
在(1)中的反比率函数图象上,其中![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() .设点
.设点![]() 坐标为
坐标为![]() ,其中
,其中![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数分析式,并直接写源于变量m的取值范围;
的函数分析式,并直接写源于变量m的取值范围;
(3)在(2)的条件下,若Q坐标为![]() ,求
,求![]() 的面积.
的面积.
分析:
(1)![]()
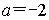
提示:设![]() 交
交![]() 轴于点
轴于点![]() ,易证
,易证![]()
由![]() ,
,![]() ,得
,得![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∴![]() ,∴
,∴![]()
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]()
则![]() ,
,![]()
∵![]()
![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
∴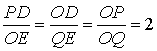
∴![]() ,∴
,∴![]() ,
,![]()
∴![]()
![]()
![]()
![]()
∴![]() (
(![]() )
)
(3)
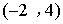
∵![]() 坐标为
坐标为![]() ,∴
,∴![]() ,∴
,∴![]() [来源:学科网]
[来源:学科网]
∴![]() ,
,![]() ,∴
,∴![]()
∴![]()
∴![]()
7.如图,双曲线![]() 与两直线
与两直线![]() 、
、![]() (
(![]() ,且
,且![]() )分别相交于
)分别相交于![]() 、
、![]() 、
、![]() 、
、![]() 四点.
四点.
(1)证明:以![]() 、
、![]()
![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(2)当![]() 为什么值时,平行四边形
为什么值时,平行四边形![]() 是矩形,请说明理由.
是矩形,请说明理由.
分析:
(1)

∵反比率函数![]() 的图象关于原点对称,过原点的直线
的图象关于原点对称,过原点的直线![]() 也关于原点对称
也关于原点对称
∴![]()
同理,![]()
∴四边形![]() 是平行四边形
是平行四边形
(2)当![]() 时,平行四边形
时,平行四边形![]() 是矩形
是矩形
理由如下:
当![]() 时,
时,![]()
∴平行四边形![]() 是矩形
是矩形
易得:![]() ,
,
由![]() 得:
得:![]()
解得:![]() ,
,![]()
∵![]() ,∴
,∴![]()
∴当![]() 时,平行四边形
时,平行四边形![]() 是矩形
是矩形
8.如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象与反比率函数
)的图象与反比率函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() (
(![]() )个单位长度后与反比率函数的图象有且只有一个公共点,求
)个单位长度后与反比率函数的图象有且只有一个公共点,求![]() 的值.
的值.
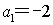
分析:(1)∵点![]() 在反比率函数
在反比率函数![]() 的图象上
的图象上
∴![]() ,即点
,即点![]() 的坐标为
的坐标为![]()
将点![]() 的坐标代入
的坐标代入![]() ,得
,得![]() ,解得
,解得![]()
∴一次函数的表达式是![]()
(2)直线![]() 向下平移
向下平移![]() 个单位长度后的表达式为
个单位长度后的表达式为![]()
联立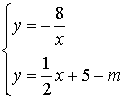 消去
消去![]() ,整理得
,整理得![]()
∵平移后的直线与反比率函数的图象有且只有一个公共点
∴![]()
解得![]() 或
或![]()
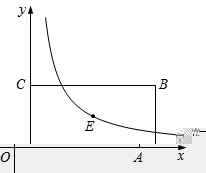
9.如图,已知矩形![]() 的一个顶点
的一个顶点![]() 的坐标是
的坐标是![]() ,反比率函数
,反比率函数![]() (
(![]() )的图象经过矩形的对称中心
)的图象经过矩形的对称中心![]() ,且与边
,且与边![]() 交于点
交于点![]() .
.
(1)求反比率函数的分析式和点![]() 的坐标;
的坐标;
(2)若过点![]() 的直线
的直线![]() 将矩形
将矩形![]() 的面积分成
的面积分成![]() 的两部分,求此直线的分析式.
的两部分,求此直线的分析式.
分析:
(1)
∵矩形![]() 的
的![]() 顶点
顶点![]() 的坐标是
的坐标是![]() ,
,![]()
![]() 是矩形
是矩形![]() 的对称中心
的对称中心
∴点![]() 的坐标为
的坐标为![]()
∵反比率函数![]() (
(![]() )的图象经过点
)的图象经过点![]()
∴![]() ,∴
,∴![]()
∴反比率函数的分析式为![]()
∵点![]() 在边
在边![]() 上,∴点
上,∴点![]() 的纵坐标为
的纵坐标为![]()
∵反比率函数![]() (
(![]() )的图象经过点
)的图象经过点![]()
∴![]() ,∴
,∴![]()
∴点![]() 的坐标为
的坐标为![]()
(2)

设直线![]() 与
与![]() 轴交于点
轴交于点![]()
矩形![]() 的面积
的面积![]()
∵直线![]() 将矩形
将矩形![]() 的面积分成
的面积分成![]() 的两部分
的两部分
∴![]()
![]()
![]()
设![]() ,则
,则![]() 或
或![]()
解得![]() 或
或![]()
∴点![]() 的坐标为
的坐标为![]() 或
或![]()
∴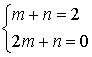 解得
解得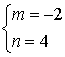
或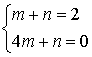 解得
解得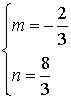
∴直线![]() 的分析式为
的分析式为![]() 或
或![]()
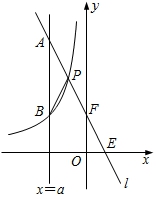
10.如图,一次函数![]() 的图象l与坐标轴分别交于点
的图象l与坐标轴分别交于点![]() 、
、![]() ,与双曲线
,与双曲线![]() (
(![]() )交于点
)交于点![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(1)求直线![]() 的分析式;
的分析式;
(![]() 2)若直线
2)若直线![]() 与
与![]() 交于点
交于点![]() ,与双曲线交于点
,与双曲线交于点![]() (不同于
(不同于![]() ),问
),问![]() 为什么值时,
为什么值时,![]() ?
?
分析:
(1)
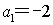
由![]() 在
在![]() 上,得
上,得![]() ,∴
,∴![]() [来源:学科网]
[来源:学科网]
∵![]() 为
为![]() 中点,∴
中点,∴![]() ,∴
,∴![]()
又∵点![]() 、
、![]() 在
在![]() 上
上
∴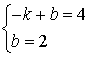 解得
解得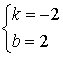
∴直线![]() 的分析式为
的分析式为![]()
(2)过![]() 作
作![]() ,垂足为点
,垂足为点![]()
∵![]() ,∴点
,∴点![]() 为
为![]() 中点
中点
由题意知,![]() 点纵坐标为
点纵坐标为![]() ,
,![]()
![]() 点纵坐标为
点纵坐标为![]() ,
,
![]() 点纵
点纵![]()
![]() 坐标为
坐标为![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() (舍去)
(舍去)
∴当![]() 时,
时,![]()







